부분 배낭 문제
<배낭 문제>
n개의 물건이 각각 1개씩 있고,
각 물건은 무게와 가치를 가지고 있으며,
배낭이 한정된 무게의 물건들을 담을 수 있을 때
최대의 가치를 갖도록 배낭에 넣을 물건들을 정하는 문제
(단위 무게당 가치가 높은 물건을 담는 것이 유리하다.)
<부분 배낭 문제(Fractional Knapsack)>
물건을 부분적으로 담는 것 허용(쪼개어 담는 것 허용)
그리디 알고리즘으로 해결
따라서 주된 아이디어는
1. 단위무게 당 가장 값나가는 물건부터 넣음
2. 통째로 배낭에 넣을 수 없다면 배낭에 넣을 수 있을 만큼만 물건을 부분적으로 배낭에 담음
알고리즘
FractionalKnapsack
입력: n개의 물건, 각 물건의 무게와 가치, 배낭의 용량 c
출력: 배낭에 담은 물건 리스트 L과 배낭 속의 물건 가치의 합 v
1. 각 물건에 대해 단위 무게 당 가치를 계산
2. 물건들을 단위 무게 당 가치를 기준으로 내림차순으로 정렬하고, 정렬된 물건 리스트를 S라고 하자.
3. L=∅, w=0, v=0
//L은 배낭에 담을 물건 리스트, w는 배낭에 담긴 물건들의 무게 합
//v는 배낭에 담긴 물건들의 가치의 합
4. S에서 단위 무게 당 가치가 가장 큰 물건 x를 가져온다.
5. while w+(x의 무게)<=C
6. x를 L에 추가
7. w=w+(x의 무게)
8. v=v+(x의 가치)
9. x를 S에서 제거
10. S에서 단위 무게 당 가치가 가장 큰 물건 x를 가져온다.
11. if C-w > 0 //배낭에 물건을 부분적으로 담을 여유가 있다면
12. 물건 x를 (C-w)만큼만 L에 추가
13. v=v+(C-w)만큼의 x의 가치
14. return L,v
value=0 # 배낭에 담긴 항목들의 가치의 합
weight_sum=0 # 배낭에 담긴 항목들의 무게의 합
item=0
while CAPACITY >= weight_sum + weight[item]:
weight_sum += weight[item]
value += (weight[item] * unit_value[item])
item += 1
partial = CAPACITY - weight_sum # 배낭에 부분적으로 담을 수 있는 무게
if partial > 0
value += (partial * unit_value[item])
수행 과정
다음 예제를 가정해보자.

배낭 용량이 40g이므로 백금과 금은 통째로 담을 수 있다.

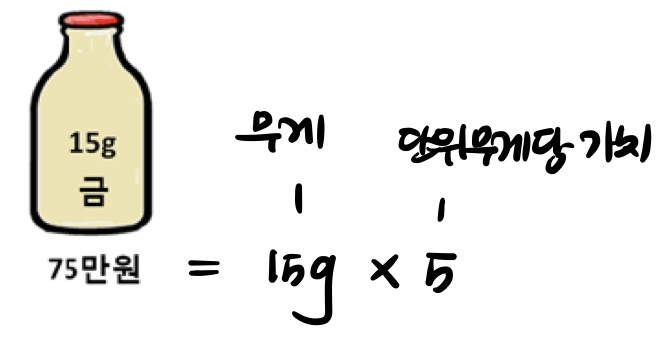
담고 나면 15g이 남지만, 그 다음으로 가치가 높은 은은 25g 있음

=> 은 담되, 15g만 담기

=> 총 60+70+6=141
시간복잡도
(Line1) n개의 물건 각각의 단위 무게 당 가치 계산 => O(n)
(Line2) 물건의 단위 무게 당 가치에 대해 정렬 => O(nlogn)
(Line5~10) while 루프 수행은 n번을 넘지 x, 루프 내부의 수행은 O(1)
(Line11~14) 각각 O(1)
==> O(n) + O(nlogn) + n*O(1) + O(1) = O(nlogn)
집합 커버 문제
n개의 원소를 가진 집합 U가 있고,
U의 부분집합들을 원소로 하는 집합 F가 주어질 때,
F의 원소들인 집합들 중 어떤 집합들을 선택하여 합집합하면 U와 같게 되는가?
<집합 커버 문제>: 집합 F에서 선택하는 집합들의 수를 최소화하는 문제
신도시 학교 배치
10개의 마을이 신도시에 만들어질 계획이다.
다음 조건이 만족되도록 학교 위치를 선정해야 한다.
1. 학교는 마을에 위치해야 한다.
2. 등교 거리는 걸어서 15분 이내여야 한다.
Q) 어느 마을에 학교를 신설해야 학교의 수가 최소가 되는가? (집합 커버 문제)
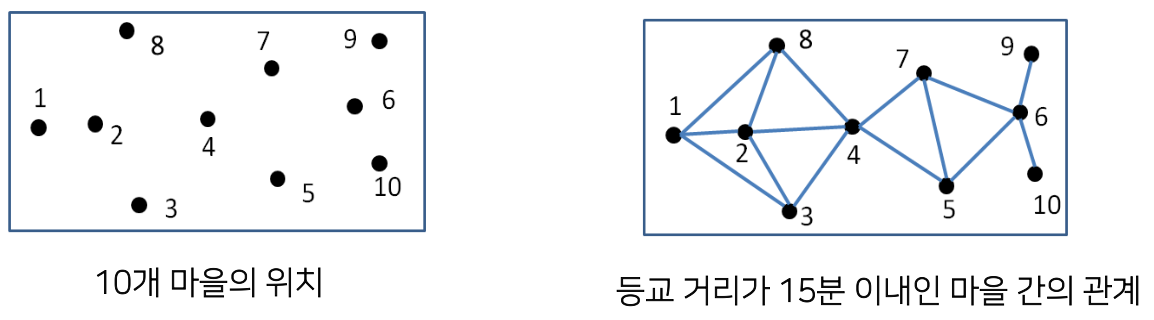
A) 2번 & 6번 마을에 학교를 배치하면 모든 마을이 커버됨
- 2번: 1,2,3,4,8 마을 학생들이 15분 이내로 등교 가능
- 6번: 5,6,7,9,10 마을 학생들이 15분 이내로 등교 가능
=> 최소 2개의 학교 필요
<집합 커버 문제로 변환>
U={1,2,3,4,5,6,7,8,9,10}
F={S1,S2,S3,S4,S5,S6,S7,S8,S9,S10}
Si = 마을 I에 학교를 배치했을 때 커버되는 마을 집합
S1={1,2,3,8}
S2={4,5,6,7}
S3={1,2,3,4}
S4={2,3,4,5,7,8}
S5={4,5,6,7}
S6={5,6,7,9,10}
S7={4,5,6,7}
S8={1,2,4,8}
S9={6,9}
S10={6,10}
=> S2∪S6=U(최적해)
최적해 찾는 방법은 위처럼 하나씩 해볼 수도 있지만,
2^n-1개를 검사해야 하므로 n이 커지면 실질적으로 불가능하다.
따라서 근사해를 찾는 것이 좋다.
알고리즘
SetCover
입력: U, F={Si}, i=1,...,n
출력: 집합 커버 c
1. C=∅
2. while U ≠ ∅
3. U의 원소를 가장 많이 가진 집합 Si를 F에서 선택
4. U=U-Si
5. Si를 F에서 제거하고, Si를 C에 추가
6. return C
수행 과정

시간복잡도
S 가 n개 있고, 각 S당 n번 비교 가능하므로 O(n^2)
U에서 Si의 원소 제거하는 데 O(n)
O(n^3) 이지만, 보통 S의 수가 증가할수록 그 속에서 비교 횟수는 줄어들기 때문에 O(n^2)라고 볼 수 있다.
작업 스케줄링
작업의 수행 시간이 중복되지 않도록 모든 작업을 가장 적은 수의 기계에 배정하는 문제
- 작업의 수: 입력의 크기이므로 알고리즘을 고안하기 위해 고려되어야 하는 직접적 요소는 아님
- 각 작업의 시작시간과 종료시간
- 작업의 길이
<작업 스케줄링>
- 빠른 시작시간 작업 우선 배정: 최적해 가능
- 빠른 종료시간 작업 우선 배정: 최적해x, 근사해o
- 짧은 작업 우선 배정: 최적해x, 근사해o
- 긴 작업 우선 배정: 최적해x, 근사해o
알고리즘
JobScheduling
입력: n개의 작업 t1, t2, ..., tn
출력: 각 기계에 배정된 작업 순서
1. 시작 시간으로 정렬한 작업 리스느: L
2. while L ≠ ∅
3. L에서 가장 이른 시작 시간 작업 ti를 가져온다.
4. if ti를 수행할 기계가 있으면
5. ti를 수행할 수 있는 기계에 배정
6. else
7. 새 기계에 ti를 배정
8. ti를 L에서 제거
9. return 각 기계에 배정된 작업 순서
m=[[0]] #기계 0으로 시작, 시작시간=0
for i in range(len(job))
j=0
allocated = False
while not allocated and j < len(m):
if job[i][0] >= m[j][0]:
m[j].append(i) #기계 j에 job i 할당
m[j][0]=job[i][1] # 기계 j의 시작(가능한) 시간은 job i의 종료시간이므로
allocate = True
j+=1
if not allocated:
m.append([0]) # 새 기계
m[j].append(i) # 기계 j에 job i 할당
m[j][0] = job[i][1] # 기계 j의 시작(가능한) 시간은 job i의 종료시간이므로
수행 과정
각 task들의 시작 시간을 오름차순으로 정렬 -> 최소한의 기계에 시간 겹치지 않도록 할당
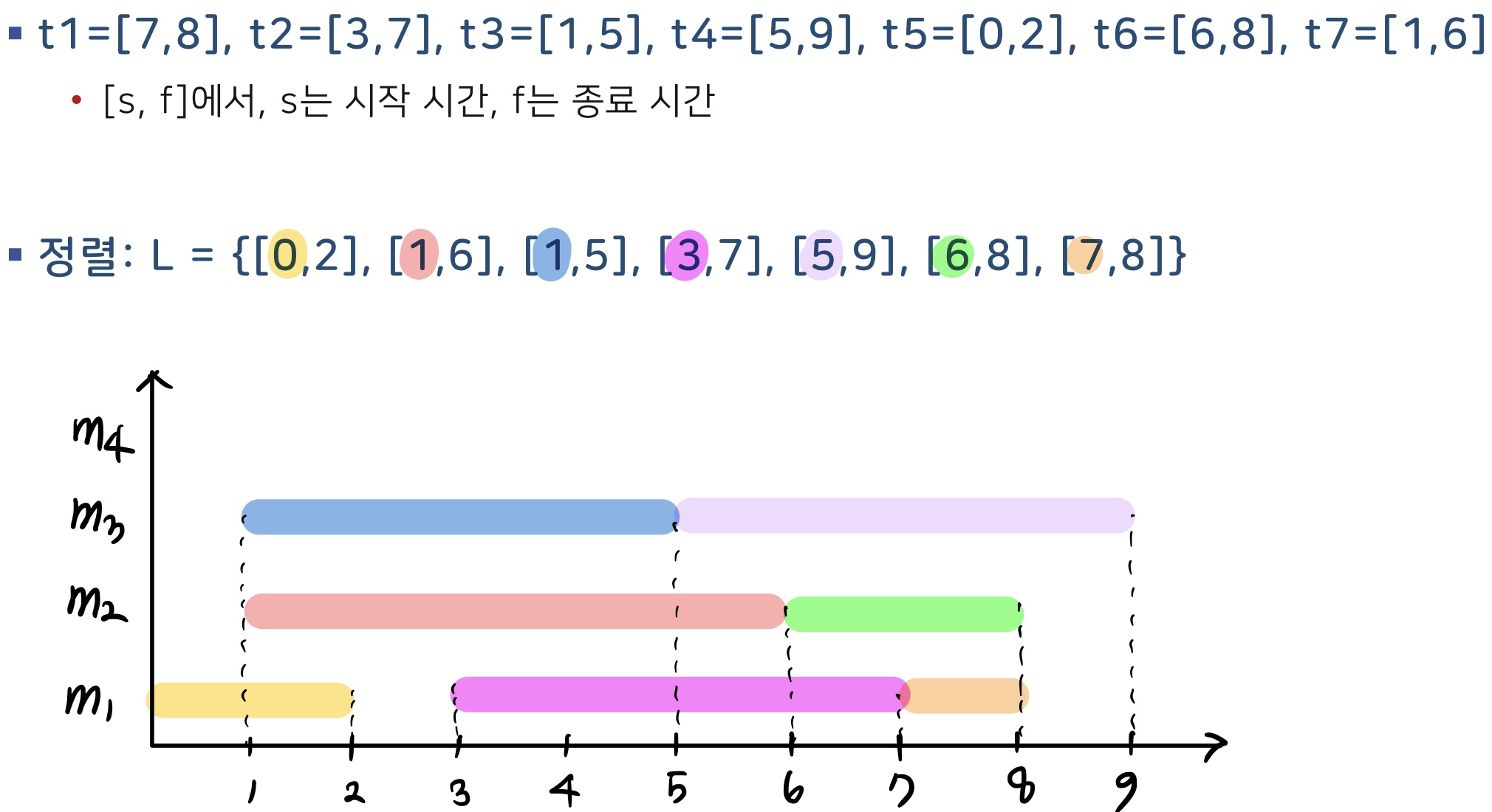
시간 복잡도
- 정렬시간 O(nlogn)
- m개의 기계 중 고르는 시간 O(m) + while 루프가 수행된 횟수는 n번 => O(mn)
==> O(nlogn) + O(mn)
추가 고려 사항
<Activity Selection>
: 그리디 알고리즘으로 1개의 host에 최대 guest 수용
Q) 기계의 수는 고정돼있고, 최대 수익을 창출하기 위해서 어떻게 task들을 배치하면 될지 스케줄링은 어떻게 해야 할까?
A)
허프만 압축
: 파일압축할 때 쓰임
파일의 각 문자가 8bit 아스키 코드로 저장되념, 그 파일의 bit수는 8*(파일의 문자 수)
파일의 각 문자는 일반적으로 고정된 크기의 코드로 표현
=> 고정된 크기의 코드로 구성된 파일을 저장하거나 전송할 때 파일의 크기를 줄이고, 필요 시 원래의 파일로 변환할 수 있으면, 메모리 공간을 효율적으로 사용할 수 있고 파일 전송 시간도 단축 가능
아이디어
- 파일에 빈번히 나타나는 문자에는 짧은 이진 코드를, 드물게 나타나는 문자에는 긴 이진 코드 할당
* 예컨대 a 50번, b 30번, c 20번, d 5번, e 100번, f 3번 나타난다면 6개의 문자를 구별하기 위해 3비트가 필요해서
a 000, b 001, c 010 d 011, e 100, f 101 이라고 할당한다면 e는 300bit를 사용하지만 f는 9bit밖에 사용하지 않기 때문에 낭비
-
알고리즘
HuffmanCoding
입력: 입력 파일의 n개의 문자에 대한 각각의 빈도수
출력: 허프만 트리
1. 각 문자 당 노드를 만들고, 그 문자의 빈도수를 노드에 저장
2. n 노드의 빈도수에 대해 우선 순위 큐 Q를 만든다.(min heap이므로 작은 것부터 꺼냄)
3. while Q에 있는 노드 수 >= 2
4. 빈도수가 가장 적은 2개의 노드 (A와 B)를 Q에서 제거
5. 새 노드 N을 만들고, A와 B를 N의 자식 노드로 만든다.
6. N의 빈도수 = A의 반도수 + B의 빈도수
7. 노드 N을 Q에 삽입
8. return Q //허프만 트리의 루트를 리턴
수행 과정
각 문자의 빈도수에 대해
A: 450
T: 90
G: 120
C: 270
(Line 2) 우선순위 큐 Q 생성
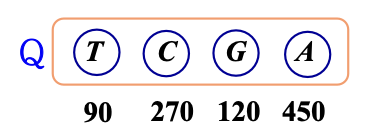
(Line 3) Q에서 'T'와 'G'를 제거 -> T,G의 새 부모 노드를 Q에 삽입

이때 T를 제거하면

G를 제거하면
210(90+120)이라는 새로운 노드를 삽입하면

트리 특성대로 정렬하면 다음과 같다.

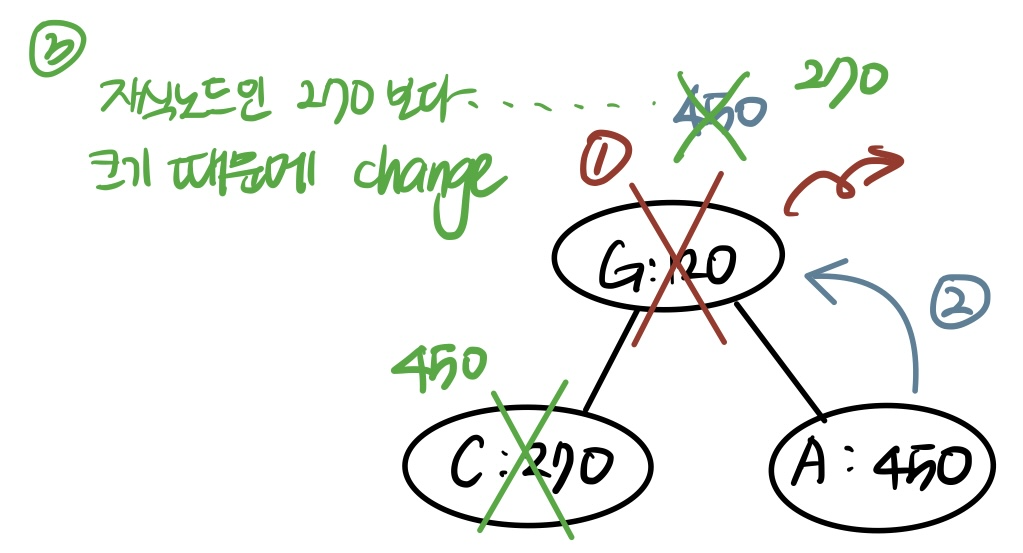
(Line3) Q에서 T와 G의 부모 노드와 C를 제거 -> 새 부모 노드를 Q에 대입
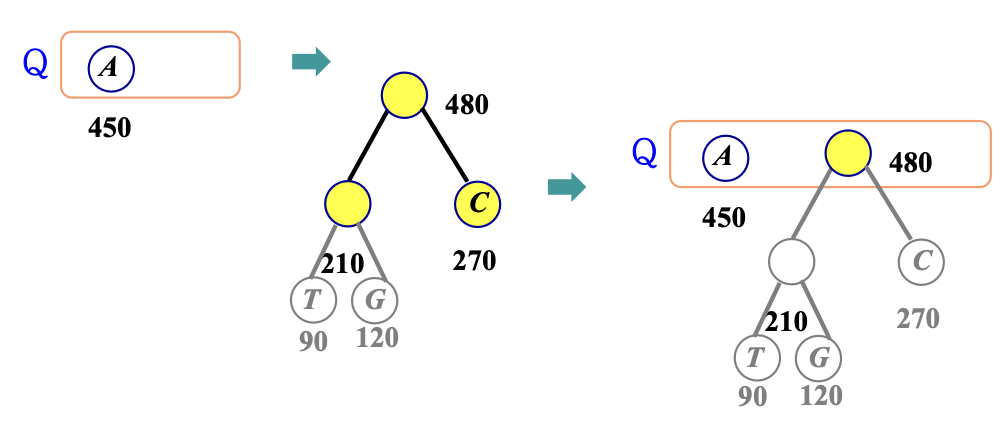
210을 뺌 -> 270이 루트가 됨

270을 뺌 -> 450이 루트가 됨

480(210+270)이라는 새로운 노드를 삽입하면

(Line3) Q에서 'T'와 'G'의 부모 노드와 'C'를 제거 -> 새 부모 노드를 Q에 삽입

450을 뺌 -> 480이 루트가 됨

480을 뺌

930(450+480)이라는 새로운 노드를 삽입

=> 완성
압축률

결과, 단말노드에만 문자가 있다.
밑으로 내려갈수록 더 큰 비트수의 이진코드가 부여된다.
- A(450): 0
- T(90): 100
- G(120): 101
- C(270): 11
=> 압축된 파일은 bit 수: (450*1)+(90*3)+(120*3)+(270*2)=1620bits
But,, 아스키코드로 된 파일 크기는 (450+90+120+270)*8=7440bits
===> 따라서 원래의 약 1/5 크기로 압축됨 !!
복호화
"10110010001110101010100" 로 압축되었다면 이것을 압축 해제해보자.
=> 101/100/100/0/11/101/0/101/0/100
=> G T T A C G A G A T
시간 복잡도
(Line1) n개의 노드를 만들고, 각 빈도수를 노드에 저장 => O(n)
(Line2) n개의 노드로 우선순위 큐 Q를 만든다. => 힙 사용하면 O(n)
(Line3~7)
- 최소 빈도수를 가진 노드 2개를 Q에서 제거하는 힙의 삭제 연산 & 새 노드를 Q에 삽입하는 연산 => O(logn)
- while-루프는 (n-1)번 반복
-> (n-1)*O(logn)
(Line8) 트리의 루트를 반환하는 것이므로 O(1)
=> O(n)+O(n)+O(nlogn)+O(1)=O(nlogn)
| Kruskal | Prim | Dijkstra | 부분 배낭 | 집합 커버 | 작업 스케줄링 | 허프만 압축 | |
| 시간 복잡도 | O(mlogm) | O(n^2) | O(n^2) | O(nlogn) | O(n^3) | O(nlogn)+O(mn) | O(nlogn) |
'학교 강의 > 컴퓨터알고리즘' 카테고리의 다른 글
| [Chapter5] 동적 계획 알고리즘 (0) | 2025.04.28 |
|---|---|
| [Chapter4] 그리디 알고리즘(1) (0) | 2025.04.26 |
| 선택 문제 (0) | 2025.04.24 |
| 퀵 정렬 (0) | 2025.04.24 |
| 합병 정렬 (0) | 2025.04.23 |



